

정렬 - quick, merge자료구조+알고리즘2022. 5. 29. 01:55
Table of Contents
퀵 정렬 - Quik sort
- 분할 정복(Divide and Conquer)을 이용해서 배열을 정렬하는 알고리즘
- 배열에서 기준(pivot)을 정해서 기준보다 작은 집합과 큰 집합으로 나누고(Divide) 그 사이에 기준을 위치시킨다.
- 작은 집합과 큰 집합을 대상으로 재귀호출하여 정렬(Conquer)한 뒤 결과를 합치면 정렬된 배열을 구할 수 있다!
- 시간 복잡도는 최선일 때 O(NlogN) 최악일 때(내림차순으로 정렬되어 있거나 오름차순으로 정렬되어있을 때) O(N^2)
예시
1단계
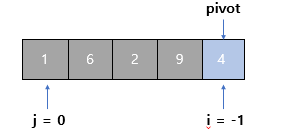
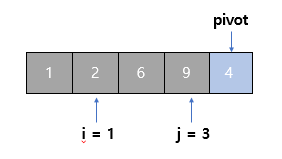
- 마지막 원소인 4를 기준(pivot)으로 정하고 pivot보다 작은 집합의 인덱스 i를 -1로 설정한다 (맨 왼쪽 인덱스-1)
→ i보다 같거나 작은 인덱스에 해당하는 값은 전부 pivot보다 작은 값이다 - j는 pivot에 해당하는 인덱스를 제외한 마지막까지 값을 비교하기 위해서 순차적으로 올라가는 인덱스
→ j를 0에서 3까지 살펴본다 (4에 해당하는 인덱스는 pivot의 인덱스)
2단계
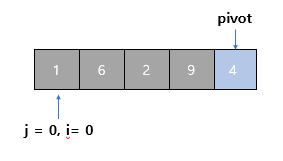
- j = 0 이므로 현재 살펴보는 값은 1이다
- 1이 pivot(4)보다 작으므로 i를 1증가시켜서 0으로 만든다.
- i 와 j의 위치를 바꾼다 → i와 j가 같아서 아무 일도 일어나지 않는다!
- (i = 0, j = 0)
3단계
- j를 1 증가시켜서 1로 만든다. 현재 살펴보는 값은 6이다.
- 6은 pivot보다 크므로 다음 단계로 넘어간다
- (i = 0, j = 1)

4단계
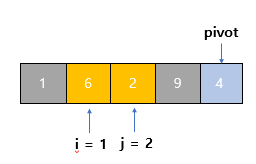
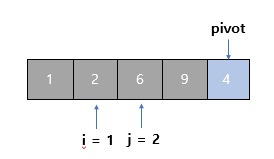
- j를 1 증가시켜서 2로 만든다. 현재 살펴보는 값은 2다.
- 2가 pivot보다 작으므로 i를 1 증가시켜서 1로 만든다.
- i와 j의 위치의 값을 바꾼다
- (i = 1, j = 2)
5단계
- j를 1 증가시켜서 3으로 만든다. 현재 살펴보는 값은 9다.
- 9는 pivot보다 크므로 다음 단계로 넘어간다.
- (i = 1, j = 3)
6단계
- j를 0부터 3까지 모두 살펴봤다!
- i보다 작거나 같은 인덱스에 해당하는 값들은 pivot보다 작은 값들이므로 i+1의 값과 pivot의 값을 바꾼다!
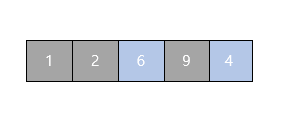
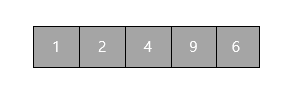
7단계
- 4를 제외한 [1, 2]와 [9, 6]을 대상으로 1~6단계를 반복한다

소스코드
def quicksort(lst, start, end):
def partition(part, left, right):
pivot = part[right]
i = left - 1
for j in range(left, right):
if part[j] <= pivot:
i += 1
part[i], part[j] = part[j], part[i]
part[i + 1], part[right] = part[right], part[i + 1]
return i + 1
if start >= end:
return None
p = partition(lst, start, end)
quicksort(lst, start, p - 1)
quicksort(lst, p + 1, end)
return lst
a = [4, 2, 6, 1, 9]
quicksort(a, 0, len(a) - 1)
print(a)병합 정렬 - merge sort
- 분할 정복 방법에 속하는 정렬 방법이다.
- 분할 된 배열들을 합병하는 과정에서 추가적인 리스트가 필요하다
- 시간 복잡도는 O(NlogN)을 보장한다!
과정
- 배열을 절반으로 분할해서 두 배열로 나눈다.
- 분할된 배열의 길이가 1이나 0이 아니라면 1번 과정을 되풀이한다.
- 인접한 분할된 배열끼리 정렬하며 병합한다 → 만약 배열의 길이가 1이나 0이라면 이미 정렬된걸로 간주!
- 원래 배열 길이가 될 때까지 3번 과정을 반복한다
예시
- [4, 6, 2, 9, 1]을 병합 정렬하는 예시!
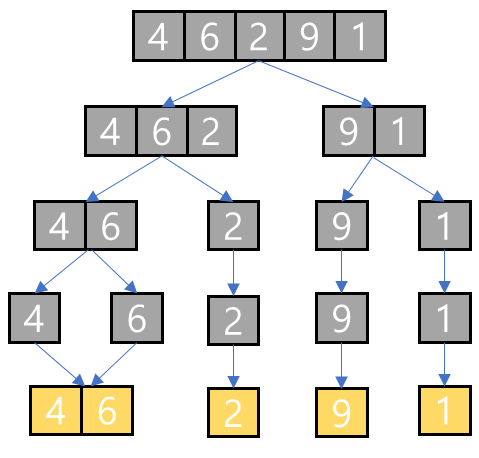
분할
- 각 배열의 요소가 한개 혹은 두개가 될 때까지 재귀적으로 분할한다.
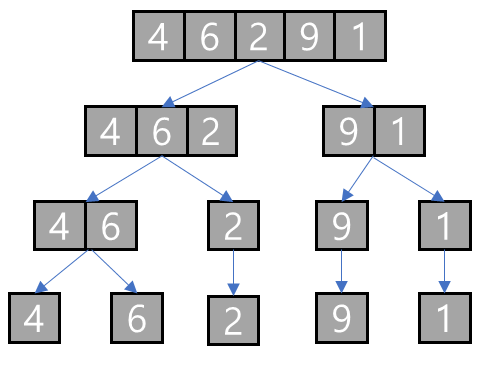
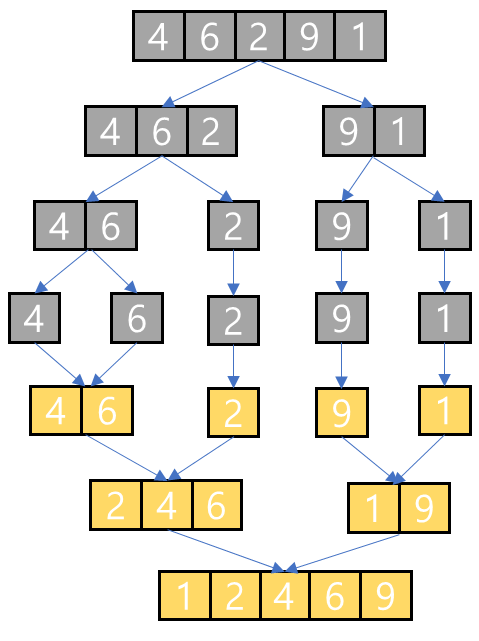
병합
- 빈 배열 a=[ ]을 하나 준비하고 b=[4]과 c=[6]의 첫번째 인덱스부터 비교해 나간다.
- 4 < 6 이므로 빈 배열에 4를 추가해서 a=[4]를 만든다.
- b=[4]를 더 이상 탐색할 수 없으므로 a=[4]에 c의 남은 원소들 [6]을 추가한다 → a=[4, 6]
- a = [4, 6]을 리턴한다
- 빈 배열 a=[ ]을 하나 준비하고 b=[2]과 c=[ ]의 첫번째 인덱스부터 비교해 나간다.
- c=[ ]를 더 이상 탐색할 수 없으므로 a=[ ]에 b의 남은 원소들 [2]를 추가한다 → a=[2]
- a=[2]를 리턴한다
- 9와 1도 위와 같은 방법으로 병합한다.
- 빈 배열 a=[ ]을 하나 준비하고 b=[4, 6]과 c=[2]의 첫번째 인덱스부터 비교해 나간다.
- 4 > 2 이므로 빈 배열에 2를 추가해서 a=[2]를 만든다.
- c=[2]를 더 이상 탐색할 수 없으므로 a=[2]에 b의 남은 원소들 [4, 6]을 추가한다 → a=[2, 4, 6]
- a = [2, 4, 6]을 리턴한다
- 빈 배열 a=[ ]을 하나 준비하고 b=[9]과 c=[1]의 첫번째 인덱스부터 비교해 나간다.
- 9 > 1 이므로 빈 배열에 1를 추가해서 a=[1]를 만든다.
- c=[1]를 더 이상 탐색할 수 없으므로 a=[1]에 b의 남은 원소들 [9]를 추가한다 → a=[1, 9]
- a = [1, 9]을 리턴한다

- 빈 배열 a=[ ]을 하나 준비하고 b=[2, 4, 6]과 c=[1, 9]의 첫번째 인덱스부터 비교해 나간다.
- 2 > 1 이므로 빈 배열에 1를 추가해서 a=[1]를 만든다.
- 2 < 9 이므로 a=[1]에 2를 추가해서 a=[1, 2]를 만든다.
- 4 < 9 이므로 a=[1, 2]에 4를 추가해서 a=[1, 2, 4]를 만든다.
- 6 < 9 이므로 a=[1, 2, 4]에 6을 추가해서 a=[1, 2, 4, 6]를 만든다.
- b를 더 이상 탐색할 수 없으므로 c의 남은 요소들 [9]를 a=[1, 2, 4, 6]에 추가해서 [1, 2, 4, 6, 9]를 만든다.
- a = [1, 2, 4, 6, 9]을 리턴한다
소스코드
def mergesort(lst):
def merge(arr1, arr2):
result = []
i = j = 0
# 두 배열의 원소가 모두 존재할 때는 작은 값을 하나씩 추가해줌
while i < len(arr1) and j < len(arr2):
if arr1[i] < arr2[j]:
result.append(arr1[i])
i += 1
else:
result.append(arr2[j])
j += 1
# arr1 이 남았으면 result에 arr1의 남은 원소 추가
while i < len(arr1):
result.append(arr1[i])
i += 1
# arr2 이 남았으면 result에 arr2의 남은 원소 추가
while j < len(arr2):
result.append(arr2[j])
j += 1
return result
if len(lst) <= 1:
return lst
mid = len(lst) // 2
L = lst[:mid]
R = lst[mid:]
return merge(mergesort(L), mergesort(R))
a = [4, 6, 2, 9, 1]
mergesort(a)
print(a)
'자료구조+알고리즘' 카테고리의 다른 글
| cmp_to_key / 커스텀 정렬 (0) | 2022.05.30 |
|---|---|
| 이진 탐색 (0) | 2022.05.29 |
| 정렬 - bubble, selection, insertion (0) | 2022.05.27 |
| 이진트리 (0) | 2022.05.23 |
| 백트래킹, N-Queen (0) | 2022.05.22 |

@덕구공 :: Duck9s'
주니어 개발자에욤
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!


